Contacte
Autor: Dr. Josep Maria Rabella. Universitat de Barcelona
Promotor: Institut Cartogràfic de Catalunya, 2013
sinònim: escala cartogràfica
cs escala; fr échelle; it scala; en scale; de Maßstab, Skala
SUMARI
- Escala de reducció, escala d'ampliació i escala natural
- Escala numèrica
- Escala d'equivalències
- Escala gràfica
- La cartografia impossible i el factor escala
- Escales imprecises i escales variables
- Altres tipus d'escales
- Temes relacionats
- Referències
- Lectures recomanades
Relació matemàtica lineal que és establerta entre les distàncies mesurables sobre un mapa, o qualsevol altre document cartogràfic, i les distàncies corresponents mesurades sobre el terreny representat.
Si tenim en compte que un mapa es caracteritza, sobretot, per ser una representació proporcional del territori i per les potencialitats universals del mètode comparatiu que se'n deriven (comparació gràfica en aquest cas), s'entén que l’escala cartogràfica constitueixi una variable de primordial importància ja que, justament, especifica el grau d’aquesta proporcionalitat, és a dir, la clau de la pròpia essència en la representació de fenòmens en cada mapa.
Escala de reducció, escala d'ampliació i escala natural
Habitualment, sobretot en el context de la geografia, de l'arquitectura o la enginyeria, les informacions es representen cartogràficament amb les seves dimensions considerablement reduïdes per tal de copsar conjunts extensos, i en conseqüència els mapes, cartes i plànols són aixecats en escales de reducció (1:100, 1:10 000, 1:500 000). Però en determinats oficis que treballen en l'entorn de la miniaturització, com la joieria o la micromecànica, els projectes i els seus desenvolupaments gràfics solen haver de ser representats de forma detallada i augmentada, amb escales d'ampliació (5:1, 100:1, etc.). Quan una representació gràfica és duta a terme sense alterar les dimensions de l'original, és a dir, sense reduccions ni ampliacions, manté el què s'anomena una escala natural (1:1)
Escala numèrica
L’escala sol ser expressada principalment de manera matemàtica (escala numèrica) en forma de fracció amb la unitat com a numerador, per exemple, 1:10 000 (de forma preferent), o bé 1/10 000. És a dir, l'escala és la fracció que especifica per quin valor han estat dividides les distàncies del territori en ser cartografiades. En un llenguatge molt elemental i escolar seria el "nombre de vegades que s'ha empetitit el territori". La simple comprensió correcte d'aquest concepte explica sobradament l'absència d'unitats mètriques en aquest tipus d'expressió numèrica.
Tres formes d'expressió habitual de l'escala numèrica.
Corregint un error massa estès i, fins i tot a voltes “ben erròniament explicat”, segons el qual “l’escala 100 000, per exemple, seria més gran que la 2 000” [sic], cal insistir en el fet que una escala gran és la que ha reduït relativament poc el territori i una escala petita representa una gran reducció, necessària si es vol cobrir de cop una gran extensió de terreny. L'error deriva de la parla habitual en citar sovint l’escala, abreujadament, sense fer esment de la unitat del numerador, per exemple dient “escala 50 000”, [sic], ometent indegudament la unitat del numerador i oblidant que aquest número citat es refereix al divisor i que quant major és el divisor l’escala queda més reduïda. D’altra banda, s’ha de subratllar que el concepte de petita, mitjana i gran escala és sempre relatiu, sense llindars mai establerts rígidament per cap convencionalisme, ja que, depèn en bona part del context professional en què s'apliquin els termes: no és el mateix l’escala d’un projecte de joieria o rellotgeria que el d’un altre d’arquitectura o el de la geografia o la cosmografia. En un context típicament geogràfic, les escales entre 1:10 000 i 1:50 000 solen ser habitualment considerades relativament mitjanes. Però, en qualsevol cas, sí pot ser afirmat amb rotunditat que l’escala 1:100, per exemple, és més gran i de més detall que l'escala 1:100 000, i encara més que l’escala 1:40 000 000 que podria correspondre a tot un globus terràqüi de sobretaula.
Escala d'equivalències
L'escala cartogràfica també permet ser expressada literalment de la manera anomenada escala d’equivalències, descrivint l’equivalència establerta entre una determinada magnitud lineal del mapa i la corresponent mesurada sobre el territori representat, quasi sempre, està clar, en unitats mètriques diferents. Freqüentment, aquesta explicació descriptiva acompanya i complementa, sobretot en mapes oficials, l’escala numèrica: “escala 1:50 000, on 1 cm equival a 500 m”, o bé “escala 1:25 000, on 1 cm al mapa correspon a 250 m sobre el terreny” o tal vegada “escala 1:25 000, on 4 cm equivalen a 1 km”.
Escala expressada literalment en forma d'equivalència.
Escala gràfica
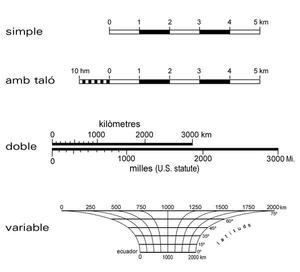
En el context, gràfic per excel·lència, que constitueix la cartografia, resulta també especialment útil i pertinent expressar l'escala en forma d’un segment traçat a la llegenda i acotat amb el seu valor corresponent al territori (escala gràfica), cosa que implica l'avantatge d'oferir una referència perceptiva ràpida, i que, en el cas d'ampliació o reducció fotomecànica del document a l'hora de ser editat, aquesta forma d'indicació gràfica de l'escala, traçada conjuntament i solidària amb la representació cartografiada, segueixi tenint vigència. L’escala gràfica admet, si és necessari, més d'un tipus d'unitat de mesura, i cal parlar d'escales gràfiques dobles (o triples), quan les distàncies sobre el segment gràfic s'expressen a la vegada, però separadament, en dues (o més) unitats mètriques alternatives, com ara quilòmetres i milles.
Quatre tipus d'escales gràfiques utilitzades habitualment en cartografia moderna.
En les anàlisis i lectures de mapes editats, freqüentment és detectat un error incomprensible i massa habitual en les escales gràfiques, que consisteix en presentar el segment grafiat amb una longitud innecessàriament preestablerta i arrodonida (per exemple: 1 cm) que després pot resultar representar un valor de distància sobre el territori absolutament rar i no arrodonit. Lògicament, s'hauria de procedir a la inversa: traçar el segment amb una longitud calculada per tal que representi una distància de valor comprensiu, fàcil i arrodonit del territori (100 m, 1 000 m, 100 km o 10 000 km, per exemple). En el cas de mapes d’escales numèriques ja arrodonides (cosa sempre desitjable per la facilitat d'ús) el valor del segment és més probable que pugui també resultar arrodonible.
Tres exemples d'escales gràfiques inadequades amb valors desconcertants i incòmodes d'utilitzar.
Escala gràfica triple en un mapa antic de Catalunya, de Ramon Yndar, de 1830.
Escala gràfica doble, en km i Mi., en un mapa d'un atles modern, WESTERMANN/RAND McNALLY: Internationaler Atlas. Chicago, 2000.
Escales gràfiques en un mapa del Principat de Catalunya de 1740, expressades amb 3 unitats mètriques diferents.
Basant-se precisament en aquest darrer tipus d’anotació de l’escala gràfica, s’elaboren regles i dispositius amb graduacions corresponents a diverses escales (quasi sempre de valors arrodonits: 1:200; 1:250; 1:500, etc.) que s'anomenen escalímetres i que poden facilitar eficaçment la lectura dels mapes impresos i l'amidament directe sobre ells. Evidentment, les unitats mètriques a aplicar en la lectura de l'escalímetre (m, hm, km...) ha de ser especificada, però resulta deduïble amb facilitat a partir de la informació donada per l'escala numèrica o, encara més fàcil, per l'escala gràfica del propi mapa si hi consta (vegeu l'apartat escalímetre).
El martell i pic és un dels recursos més tradicionals dels geòlegs per a suggerir l'escala del context captat en una fotografia. ICC i IGC: Atles Geològic de Catalunya. Barcelona, IGC i ICC, 2010.
Un altre fascinant exemple d'escala gràfica per mitjà d'una marieta inclosa en aquest petit bloc diagrama il·lustrat per Peter Van Dusen sobre l'efecte de l'impacte de les gotes d'aigua de la pluja. MARSH, W. M. i DOZIER, J.: Landscape. An Introduction to Physical Geography. Reading, Massachusetts, Addison-Wesley, 1981. ISBN: 0-201-04101-4.
Una variant de la tradicional escala gràfica, interessant, només aproximativa però molt intuïtiva, sobretot en el cartografiat de grans extensions territorials, consisteix a acompanyar-la amb la inclusió del cartografiat d'un contorn d'un determinat territori menor, proper, ben conegut i fàcilment identificable, a la mateixa escala, de manera que, per simple comparació visual, el lector tingui una percepció immediata de les magnituds representades. És el què podria ser anomenada una escala gràfica territorial, que constitueix un dels molts i valuosos recursos didàctics de la cartografia, emprat ja en l'avançada cultura escolar helvètica de principis del segle XIX, i en aquell cas concretat amb la silueta territorial de Suïssa com a referència per a tots el seus ciutadans que la reconeixen: sota el contorn consta "Suïssa a la mateixa escala".
Un recurs magistral, intuïtiu i antic, recuperat en un atles escolar actual, és el mapa auxiliar d'un territori fàcilment identificable que funciona com a verdadera escala gràfica a comparar amb els territoris cartografiats. En aquest cas, la silueta de la Península Ibèrica dins la llegenda del mapa d'Amèrica. RABELLA, J. M.: Atles del món. Barcelona, Edicions 62, 2008. ISBN: 978-84-297-6117-7.
La cartografia impossible i el factor escala
De forma un tant paradoxal, cal parar compte en el fet que, deixant a part els globus terraqüis, una representació cartogràfica exacte del territori sobre un mapa pla resulta una tasca impossible. Efectivament, en qualsevol mapa pla, l'escala teòricament mai no pot resultar exacta, ja que la transformació de la superfície corba de la Terra a la superfície plana del mapa implica alteracions dimensionals absolutament inevitables, plantejades i estudiades en el gran tema de les projeccions. En mapes d'escala molt gran, amb cobertures territorials molt poc extenses, (fulls topogràfics d'escala 1:25.000 en fusos de projecció UTM, per exemple) aquestes alteracions poden resultar insignificants per a la majoria de finalitats quotidianes i, fins i tot, no superant uns pocs quilòmetres (3, 5, 10...) el propi aixecament topogràfic pot de vegades no contemplar aquest fet i considerar la Terra plana a efectes pràctics i aproximatius. Precisament l'anomenat factor d'escala (FE) fa referència a aquest fet, en expressar la relació entre el que seria l'escala nominal o principal, exacte, en una representació cartogràfica esfèrica, i l'escala real (verdadera) amb alteració que resulta sobre un lloc i una direcció concreta en el corresponent mapa pla. El factor d'escala en un mapa topogràfic d'escala gran en projecció UTM, per exemple, pot tenir un valor molt ajustat entre 0,9996 i 1,00158. No obstant, en el cartografiat de territoris molt més extensos, el problema creix de forma notable i és imprescindible optar per la projecció més convenient en cada cas (projeccions afilàctiquesi projeccions discontínues o altres estratègies) a l'hora de l'aixecament territorial, i tenir-ho en compte a l'hora de la lectura correcte del mapa, de vegades mitjançant escales variables, degudament indicades, o altres recursos.
Escales imprecises i escales variables
En la representació de grans territoris, sobretot en mapes continentals i encara més en planisferis, l'escala pot ser tant variable que invalidi la possibilitat d'especificar-la, encara que, lamentablement no sempre això és tingut en compte pels editors. Sovint, en aquests casos s'hauria de parlar de forma reduccionista d'escala sobre l'equador, sobre el meridià central de la projecció, sobre tots els paral·lels o les altres especificacions que siguin pertinents en cada cas. En aquest sentit, en les projeccions cilíndriques resulta habitual mostrar una escala gràfica variable orientativa adaptable per a cada latitud concreta del planisferi. En mapes en projeccions afilàctiques, d'altra banda, podria ser acceptable parlar prudentment, si més no, d'escala aproximada o escala mitjana. Una cosa relativament semblant passa en la presentació de fotografies aèries o imatges de satèl·lit no corregides on, a les deformacions degudes a la curvatura de la Terra, s'hi afegeixen els desplaçaments planimètrics i els canvis d'escala produïts, sobretot, a causa del relleu del territori i, per tant, només pot al·ludir-se a una escala aproximada (o nominal), advertint en tot cas l'usuari de la falta de precisió planimètrica i la improcedència d'utilitzar el document com una base amb un valor mètric plenament cartogràfic. D'aquesta dificultat se'n deriva el gran valor de les ortofotografies, fotogrames corregits planimètricament i amb ple valor mètric cartogràfic i, des de fa algunes dècades, fàcilment generades amb avançades tecnologies digitals.
Altres tipus d'escales
En cartografia molt rarament es fan servir altres escales diferents de les aritmètiques i lineals, però en el terreny de la gràfica (i en els gràfics dels cartodiagrames i en els símbols proporcionals dels mapes temàtics) poden ser utilitzades escales de superfície (valor quadrat de les escales lineals) i de vegades encara escales de volum (valor cúbic de les escales lineals), circumstància aquesta que, per excepcional, ha de quedar ben indicada, de manera destacada i inequívoca.
Altre tipus d'escala és l'escala logarítmica, basada en el valors del logaritmes dels nombres naturals, i que és usada en diagrames estadístics. En gràfics de coordenades cartesianes es pot optar per emprar escales logarítmiques en els dos (o tres) eixos, o bé en un sol eix, mantenint en l'altre (o altres) una escala aritmètica (aquests anomenats a voltes gràfics semi-logarítmics).
Un gràfic amb l'eix de les ordenades en escala logarítmica per mostrar si les taxes de creixement es mantenen constants (en forma de recta), o si augmenten o disminueixen i en quin ritme ho fan, segons avancin amunt o avall, i mantinguin els creixements constants o canviants en forma de corba. Aquests gràfics reben sovint el nom de semi-logarítmics. Atles escolar del País Valencià. Universitat de València, 1997
Es tracta de poder representar en un mateix gràfic valors molt dispars, al preu de falsejar la percepció d'autèntica proporcionalitat gràfica o bé, en un context de major nivell estadístic, per a destacar les tendències de taxes de creixement amb els seus significats: no només els augments o decreixements absoluts, sinó també els valors relatius: increments, estabilitats o pèrdues en els propis índexs.
En la presentació de perfils i talls topogràfics, d'altra banda, cal parlar d'escala horitzontal i d'escala vertical, diferenciant-les sobretot quan, com passa freqüentment, aquesta última és més gran (exagerada) que la primera.
En el context de l'expressió gràfica i cartogràfica encara seria oportú parlar d'escales gràfiques aplicades als pendents territorials, a les llegendes dels símbols proporcionals o a moltes altres variables, i fins i tot aplicades al vector temps, com és freqüent veure en les cronologies de les llegendes dels mapes geològics. De fet, tal vegada és ací on més es relacionen i complementen la cartografia amb l'expressió dels gràfics i diagrames.
Temes relacionats
Referències
McMASTER, Robert i SHEA, K.Stuart: Generalization in Digital Cartography. Washington, Association of American Cartographuers, 1992. ISBN: 8-89291-209-X
RAISZ, Erwin: General Cartography. 1938 (1a edició). Traducció en castellà: Cartografía. Barcelona, Omega, 1953, 2005. ISBN 84-282-0007-6.
ROBINSON, Arhur H. i altres: Elements of Cartography. (6a ed.) Nova York, John Wiley & Sons, Inc., 1995. ISBN: 0-471-55579-7. Trad. al castellà:Elementos de Cartografía. (5a ed.) Barcelona, Omega, 1987. ISBN: 84-282-0768-2.
ROSA i TRIAS, Elisabet: Conceptes, tècniques i problemes de la generalització cartrogràfica. Barcelona, Universitat de Barcelona, Tesis doctorals, 2000. ISBN 9788469221044.
STOTER, J. i altres: A study on the state-of-the-art in automated map generalisation implemented in commercial out-of-the-box software. Workshop sobre generalització i múltiple representació de la Comissió de Generalització de la ICA. Montpeller, 2008.
SWISS SOCIETY OF CARTOGRAPHY: Cartographyc Generalisation: Topographic Maps. Cartographyc Publication Series, núm, 2, 1977. ISBN: 978-3-540-69653-7
Lectures recomanades
BERTIN, ECKERT, INHOF i altres: El mapa com a llenguatge geogràfic. Recull de reflexions contemporànies (s. XX). Barcelona, Institut d’Estudis Catalans i Instituto Geográfico Nacional, 2010. ISBN: 978-84-416-1558-8 i 978-84-92583-82-9.
SCHAEFER, Fred K.: “Excepcionalism in Geography. A Methodological Examination” a Annals of the Association of American Geographers, vol. 43, núm. 3, setembre de 1953, pàg. 226 a 249. s/ISBN
